La ecuación de Schrödinger en acción
La ecuación de Schrödinger determina la función de onda de un sistema. En particular, aplicado a un electrón, describe cómo se comporta cuando está un entorno específico descrito por la energía potencial V(x), y unas condiciones de contorno. Según la expresión de este potencial y condiciones, la ecuación es más o menos sencilla de resolver. Vamos a ver un par de casos sencillos, de donde se deducen consecuencias importantes.
El electrón libre
La situación más simple es cuando un electrón no se halla sometido a ningún tipo de interacción. En este caso, la energía potencial es nula, y se habla de un “electrón libre”. La ecuación de Schrödinger independiente del tiempo queda entonces como
El electrón libre
La situación más simple es cuando un electrón no se halla sometido a ningún tipo de interacción. En este caso, la energía potencial es nula, y se habla de un “electrón libre”. La ecuación de Schrödinger independiente del tiempo queda entonces como
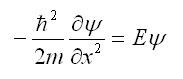
La solución a esta ecuación es:
Por cada valor de k, hay una autofunción, o estado del sistema. El significado de la variable k está relacionado con el momento cinético. Al sustituir la función de onda en la ecuación de Schrödinger, se puede deducir el valor de la energía en función de la variable k:

de donde se deduce que k es proporcional al momento cinético. A la variable k se le denomina vector de onda, dado que si recordamos la expresión del momento para un fotón,

k está relacionado con la longitud de onda.
La relación entre E y k se denomina relación de dispersión, y describe los estados posibles del electrón. En el caso del electrón libre, toda su energía es únicamente la cinética, debida a su movimiento. El electrón se halla lejos de cualquier interacción y no hay ninguna condición especial sobre k o sobre E, y por tanto, el electrón puede tener cualquier valor de energía cinética. Es decir: un electrón libre no tiene cuantizada su energía, su energía es un continuo, y existen infinitos estados posibles para él.
El pozo cuántico infinito
El segundo ejemplo es llamado el pozo cuántico. La energía total del electrón siempre es la suma de su energía cinética y potencial. Si limitamos una región del espacio donde el potencial es nulo, pero fuera de éste se hace infinito, entonces el electrón se halla confinado, metido en un pozo, limitado entre las posiciones x=0 y x=L.
No tiene sentido plantear la ecuación de Schrödinger en una zona de potencial infinito, dado que el electrón nunca tendrá una energía total mayor que ésta; pero sí se puede plantear dentro del pozo. No obstante, ahora es necesario incluir condiciones de contorno: la probabilidad de encontrar al electrón en una zona donde no tiene sentido planteárselo tiene que se nula; es decir:
La solución a la ecuación de Schrödinger en la región del pozo sigue siendo la misma que para el electrón libre. Al aplicar las condiciones de contorno, sin embargo:

De la primera condición, se deduce que todas las autofunciones se describen sólo por la función seno, y no por la suma de seno y coseno, como en el electrón libre. Pero la condición más importante es la segunda: sólo puede ser cero cuando A·sen(kL)=0. Una solución es que A=0. Pero al ser el seno una función periódica, esto también ocurre cuando kL es un múltiplo entero de π. De esta forma, se revela que el vector de onda k está cuantizado: no puede existir cualquier estado, sino sólo aquellos cuyo vector de onda sea un múltiplo entero de π/L. Y como consecuencia, la energía también está cuantizada:

Es decir, aún cuando siguen existiendo infinitos estados posibles para un electrón en un pozo infinito, la energía de éstos no puede ser cualquiera, sino que está cuantizada.

Esta gráfica representa los valores de energía que puede tener una partícula dentro de un pozo infinito, representado por las dos líneas verticales azules. Superpuesta a cada energía, está puesta la función de onda correspondiente a ese estado.
La consecuencia más importante de estos dos ejemplos es entender que una partícula que se halla confinada entre dos barreras de potencial, no puede tener cualquier energía, sino que la tendrá cuantizada. Por el contrario, cuando una partícula se halla libre de cualquier interacción, no hay condiciones para su energía, sino que es continua.

El átomo de Schrödinger
¿Cuál es el potencial de energía de unos electrones en el átomo? Este potencial no es otro que el electrostático, que es inversamente proporcional a la distancia:

donde r es la distancia en el eje radial, y Z el número de protones del átomo. En este potencial se pueden ver dos zonas claramente separadas, dependiendo de la energía del electrón:

Una zona donde un electrón sería considerado “libre”, y por tanto, fuera del átomo y con energía continua (Zona A), y una zona donde el electrón se halla confinado por el potencial (Zona B), y por tanto su energía cuantizada. La solución de la ecuación de Schrödinger para este potencial es complicada, pero hace aparecer finalmente la misma cuantización que Bohr y Sommerfeld tuvieron que postular para describir los electrones del átomo.
La frontera entre las zonas A y B se denomina "nivel de vacío", es la energía de referencia respecto de la cual se refieren las otras., y representa la diferencia entre un electrón ligado, o confinado dentro del átomo, y un electrón que ha conseguido escapar. Según se toma esta referencia, las energías de los electrones ligados son negativas, mientras que la de los electrones libres son positivas.
Para arrancar un electrón de un átomo, es preciso darle una energía al menos igual a la de su ligadura. Con eso, su energía queda en el nivel de vacío. Si se le suministra más, esa energía extra se emplea en poner en movimiento al electrón, energía cinética, que al ser ya un electrón libre, no tiene ningún tipo de condición especial.



No hay comentarios:
Publicar un comentario